烦夜蛾Anophia leucomelas Linnaeus属鳞翅目Lepidoptera夜蛾科Noctuidae 。近年来在福建沿海甘薯种植区普遍发生,为害严重,已成为甘薯生产上的主要害虫之一。福建闽南、莆田沿海一带1年发生5~6代[1-2],冬季无休眠现象。常与斜纹夜蛾并发,幼虫取食叶片,为害严重时仅剩叶柄,对甘薯薯块的膨大影响较大,严重影响甘薯的产量和质量[2],为害面积逐年扩大。为了有效控制烦夜蛾在甘薯田间的发生和扩散,亟需明确该虫的空间分布和种群发展动态。目前国内对于烦夜蛾幼虫空间分布型的研究报道甚少,为此,本研究对烦夜蛾幼虫在甘薯田间的空间分布型、理论抽样数及序贯抽样等进行探讨,并对发生情况进行预测和检验,旨在为预测预报和防治提供一定的理论依据。
1 材料与方法 1.1 调查地点和方法2015年9月,在福建省福州市城门镇湖际村(北纬25°50′,东经118°46′,海拔高度5 m)甘薯田进行调查。甘薯品种为‘榕薯819’,长势良好,田间常规管理。调查时,甘薯生长处在薯块膨大期,选择长势较均一、烦夜蛾发生程度不同的8块甘薯田,每块田面积333.5 m2,采取“Z”字形进行取样,调查140株,共计1 120株,逐株记载烦夜蛾幼虫的数量。调查前,田块未喷洒农药进行防治。
1.2 空间分布型的测定调查所得的幼虫数用Excel 2003和DPS数据处理系统V7.05[3]进行统计分析,分别计算出各田块幼虫的平均数m、方差S2和平均拥挤度m*,依据聚焦度指标如丛生指数I、聚块性指数m*/m、久野指数CA、扩散指数C、负二项分布K值[4-6]、兰星平的L*/m[7]等参数的判定标准来推断烦夜蛾幼虫在甘薯田上的空间分布形式。
1.3 回归方程的检验利用Iwao的m*-m直线回归分析法[8]和Taylor幂法则[9]来分析种群的分布格局和内部结构;烦夜蛾幼虫在甘薯田的聚集原因采用Blackith的种群聚集均数λ[10]来检验。
1.4 理论抽样数的确定甘薯田间烦夜蛾幼虫在不同密度和不同误差条件下的最适理论抽样数依据Iwao理论抽样数模型[11]来确定。
目前,甘薯田中的烦夜蛾还未确立明确的防治指标,因此,本研究采用Kuno序贯抽样模型[12]:
从表 1可以看出,各项聚集度指标中,I>0,m*/m>1,CA>0,C>1,K>0,L*/m>1,按照各参数空间分布型判定标准来推断,烦夜蛾幼虫在甘薯田为聚集分布。
| 表 1 甘薯田烦夜蛾幼虫聚集度指标 Table 1 Indices on spatial distribution of A. leucomelas larvae in sweet potato fields |
甘薯田间烦夜蛾幼虫密度m和平均拥挤度m*的关系采用Iwao m*-m直线回归模型进行线性回归,由此得出m*=0.3102+1.6255m(R=0.9501),m*与m之间呈极显著相关。该模型中参数α=0.3102>0,在甘薯田间烦夜蛾幼虫个体间相互吸引,分布的基本成分是个体群;参数β=1.6255>1,可以判定烦夜蛾幼虫呈聚集分布。又由α>0,β>1可知,甘薯田间烦夜蛾幼虫种群的聚集型为一般负二项分布。
2.2.2 Taylor幂回归模型各样点的幼虫密度m和方差S2之间的关系运用Taylor幂回归模型进行线性回归,由此得出lg(S2)=1.9537+1.2196×lg(m),相关系数R=0.9871。根据lg(a)=1.9537>0,b=1.2196>1,可知烦夜蛾幼虫在甘薯田间一切密度下其空间分布型均呈聚集分布。且聚集强度与幼虫密度正相关,即随着虫口密度的增强,聚集强度随之增加。
2.2.3 聚集均数烦夜蛾幼虫在甘薯田间的聚集均数λ均小于2(表 1),根据Bliackith的聚集均数λ理论可以判断出,当地的气候条件、植株的生长状况等环境因素是引起烦夜蛾幼虫聚集的主要原因。对各样方平均数(m)和聚集均数(λ)进行相关分析,可得出方程式:λ=0.7699 m-0.0816(R=0.9857),λ与m之间呈极显著相关。由此可知,烦夜蛾幼虫的聚集均数λ随种群密度(m)的增强而升高。当田间幼虫密度≥2.703 7头·株-1时,λ≥2,聚集原因是由幼虫的聚集行为引起的,或是由幼虫本身的聚集行为与环境的差异性共同作用引起的;幼虫的密度 <2.703 7头·株-1时,λ<2,聚集原因则是由于某些环境因素所导致的。
2.3 理论抽样数公式的建立将Iwao m*-m回归模型中2个参数α =0.310 2,β=1.625 5 代入理论抽样数模型中,即可得出理论抽样数公式为:N=t2D2×1.3102m+0.6255。根据此公式,保证概率为0.95(t=1.96)情况下,允许误差 D为0.1、0.2和0.3,平均幼虫数m为0.1、0.2、0.3、0.4……3时,得出烦夜蛾幼虫在甘薯田中不同密度下的理论抽样数如表 2所示。
由表 2可知,在允许误差相同的条件下,随着虫口密度的增大,抽样数在减少。如允许误差为0.1时,虫口密度为0.2头·株-1时,抽样数为2 757株;虫口密度为2头·株-1时,抽样数减少为492株。在虫口密度相同的条件下,随允许误差的增大,抽样数在减少。如虫口密度为1头·株-1,允许误差为0.1时,抽样数为744株;允许误差为0.3时,抽样数则减少为586株。
| 表 2 烦夜蛾幼虫不同虫口密度下的最适抽样数 Table 2 Optimum sampling number on A. leucomelas larvae for varied insect population densities |
将Iwao m*-m回归模型中两个参数α =0.310 2,β=1.625 5代入Kuno的序贯抽样模型中,得出公式为:
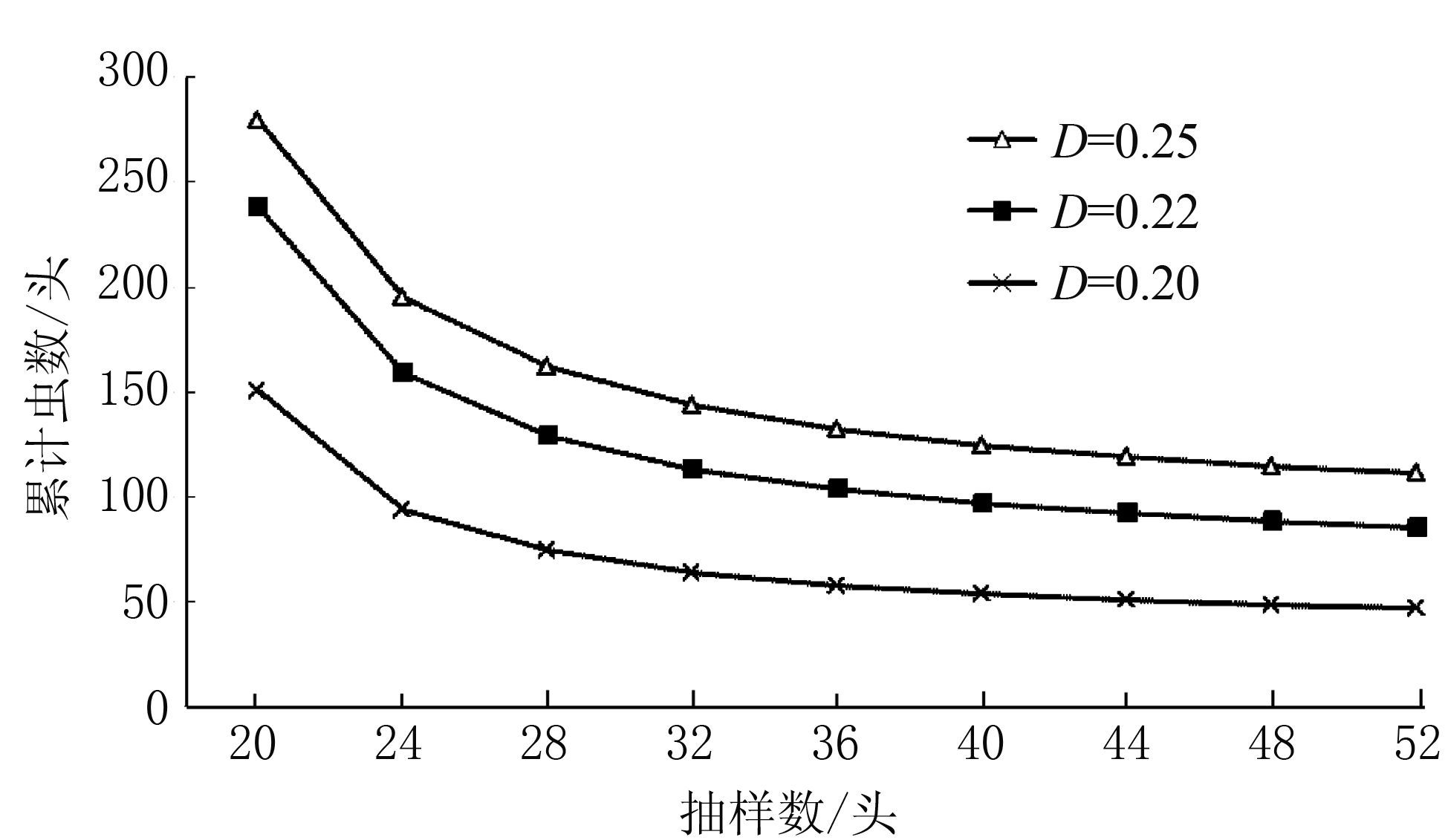
|
图 1 烦夜蛾幼虫的Kuno序贯抽样 Figure 1 Kuno sequential sampling on A.leucomelas larvae |
从6个聚集度指标、2个回归模型等可以看出,烦夜蛾幼虫在甘薯田间的空间分布型为聚集分布,分布的基本成分是个体群,个体间相互吸引,且随着虫口密度的增加聚集强度升高。通过聚集均数的分析,表明引起该虫聚集的主要原因是由某些环境因素。
利用Iwao线性回归模型中的2个参数α和β建立起烦夜蛾幼虫的理论抽样数公式和序贯抽样模型。在进行田间虫情调查时,采用最适理论抽样数和序贯抽样图,作为烦夜蛾幼虫田间虫情调查时的参照,为田间调查和预测预报提供了科学依据,对于烦夜蛾幼虫在甘薯田间种群密度估算精度的提高和分析判断田间种群的防控效果均有一定的指导意义。
烦夜蛾幼虫在甘薯田间呈聚集分布,其他虫态的空间分布型如何还有待探讨;由于目前对烦夜蛾的研究较少,要制定出合理的防治指标还需要进行大量的试验,这些问题都有待日后进一步研究。
| [1] |
黄成裕, 林本兴.
烦夜蛾生活习性的研究[J]. 昆虫知识 , 1983, 20 (4) : 165–167.
( 0) 0)
|
| [2] |
张继祖, 郑国阳, 朱志平.
福建莆田烦夜蛾的初步研究[J]. 华东昆虫学报 , 1996, 5 (2) : 40–45.
( 0) 0)
|
| [3] |
唐启义, 冯明光. 实用统计分析及其计算机处理平台[M]. 北京: 中国农业出版社, 1997 .
( 0) 0)
|
| [4] |
张孝羲, 张跃进. 农作物有害生物预测学[M]. 北京: 中国农业出版社, 2005 : 37 -49.
( 0) 0)
|
| [5] |
何平, 余爽, 王友富, 等.
西花蓟马在石榴上的空间分布型及理论抽样数[J]. 植物保护 , 2012, 38 (4) : 131–132.
( 0) 0)
|
| [6] |
张应, 崔广林, 李隆云.
胡萝卜微管蚜在灰毡毛忍冬上的空间分布格局[J]. 植物保护 , 2012, 38 (6) : 77–79.
( 0) 0)
|
| [7] |
兰星平.
种群聚集度指标回归模型在检验昆虫种群空间分布型中的应用[J]. 贵州林业科技 , 1995, 23 (1) : 40–52.
( 0) 0)
|
| [8] |
IWAO S.
Application of the m*-m method to the analysis of spatial patterns by changing the quadrat size[J]. Researches on Population Ecology , 1972, 14 : 97–128.
DOI:10.1007/BF02511188 ( 0) 0)
|
| [9] |
TAYLOR L R.
Aggregation,variance and the mean[J]. Nature , 1961, 189 : 732–735.
DOI:10.1038/189732a0 ( 0) 0)
|
| [10] |
徐汝梅, 成新跃. 昆虫种群生态学——基础与前沿[M]. 北京: 科学出版社, 2005 : 3 -17.
( 0) 0)
|
| [11] |
IWAO S, KUNO E.
Use of the regression of mean crowding on mean density for estimating sample size and the transformation of data for the analysis of variance[J]. Research Population Ecology , 1968, 10 : 210–214.
DOI:10.1007/BF02510873 ( 0) 0)
|
| [12] |
KUNO E.
A new method of sequential sampling to obtain a fixed level of precision[J]. Research on Population Ecology , 1969, 16 : 281–288.
( 0) 0)
|
 2016, Vol. 31
2016, Vol. 31